
6-16-99
The Question:
Ann Harch asked us, "What's the relative rate of rotation of eros when NEAR is in the 100km orbit?" (That is, how long does it take for the spacecraft to get back to the same longitude?)
The Answer:
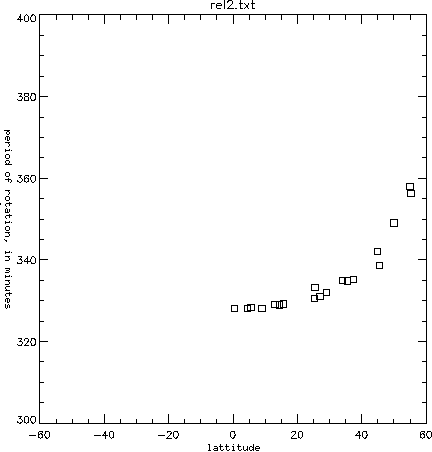
It takes between 328 and 358 minutes for eros to rotate once underneath NEAR. The period is dependent upon the latitude of the spacecraft - it is fastest when the latitude is around zero, and slowest when the latitude is at a maximum or a minimum (57 or -57 degrees for this orbit).
Here's a graph of the exact period of rotation dependent upon latitude.
How we calculated our results:
Emily: using ORBIT, I took frames every 60 seconds for one full orbit of the spacecraft around the asteroid. I saved those frames in a something.f file, and then opened the something.f file.
Method 1: I chose a starting frame with a certain longitude, and went through the .f file until I came back to a frame with that same longitude. I took the average of the latitudes during that peroid, and the differences between the times for the two frames.
Method 2: I chose a starting frame with a certain latitude, and recorded that longitude. I then moved to a frame that was taken about 20 degrees of longitude later. I recorded the difference between the longitudes, the difference between the time, and used that data to calculate how long the full orbit would have taken at that latitude. This method is more precise with respect to latitude.
Jessica: I used a different method, and got the same results. I didn't use .f files at all. I went into orbit, and used "generate MSI frames for timing" in the auto menu to get a 60 second delta between frames. Then I emacs'ed the overview file, and found the starting time where the latitude was about 0 degrees, about 10 degrees, about 20 degrees, and so on up to 60, the maximum latitude of NEAR. (My reasoning for this will be explained below: basically I expecteced for the relative orbit times to be different depending on WHERE the spacecraft was in the orbit of Eros). Anyway, I went back into orbit, and one by one, I went to the starting times of each of my 6 different latitudes. I noted the longituted that the program showed. Then I clicked "next N" until the longitude went through 360 degrees back to its starting point. I noted the time again, and that difference in time was the time it took to do a full orbit.
The times varied quite a bit. It's important to note that when I started at a 0 degree latitude, in the five and a half hour spin of of Eros, the spacecraft moved nearly 30 degrees in latitude - so it is impossible to be really precise with it (at 60 degrees, of course, the latitude almost didn't change at all, because it was at the highest point of its latitude, moving longitudinally).